功率谱估计(PSD)的实现(附MATLAB仿真程序)☆

摘要
功率谱估计是信号处理领域的重要问题之一。在实际应用中往往不能获得具体信号的表达式，需要根据有限的数据样本来获得较好的谱估计效果。
本论文研究了功率谱估计的几种常用的方法，包括经典法和参数法中的AR模型法，对每种方法的估计质量做了数学推导，给出仿真程序及仿真图，在仿真图的基础上对每种方法的性能进行了讨论。
经典法主要包括周期图法和BT法，但这两种方法都存在明显缺陷，即认为观测数据之外的数据都为零，所以对经典法中的周期图法进行了加窗，平均等修正。
从仿真图中可以看出，经典法无论是在谱分辨率还是在主瓣宽度，旁瓣幅度等方面都存在不足。AR模型法通过应用随机过程可用一白噪声通过一物理网络表示的理论，避免了经典法中除了观测数据之外的数据都为零的假设，因此能得到较好的谱估计效果。
关键字：功率谱估计；周期图；BT法；AR模型法。

ABSTRACT
Power Spectral Estimation is a fundamental topic in the signal processing field. Actually, we can’t get the precise expression of a specific signal, so we need to estimate the power spectral of a signal according to some sample data sequences.
In this thesis, some common methods of Power Spectral Estimation, such as classical spectral estimation、AR model of modern spectral estimation, are studied. The quality of each estimation method is derived, and the program and some simulated figures of these methods are also provided. In addition, the performance of each method is discussed according to the simulated figures.
Classical methods of Power Spectral Estimation mainly include The Periodogram and the BT method. But both of them have a common drawback: the data sequences, beyond the area of the observed sequences, are all presumed to zero. So the Windows and the average method are introduced to improve the quality of The Periodogram.
From the simulated figures, we see that the classical methods have some conspicuous disadvantages, no matter in the spectral resolution or the main lobe width、the side lobe amplitude. AR model, which supposed that any random processes can be expressed as white noise crossing a physical union, avoids the drawback of the classical methods. So, better results of the estimation of the power spectrum can be obtained.
Keywords: Power Spectrum Estimation；The Periodogram；the BT methods；AR model.
 
本篇论文介绍了功率谱估计的几种常用方法，包括周期图及其修正，BT法，AR模型法，给出了详细的估计步骤和估计性能，对每一种方法及相应的改进方法进行了基于MATLAB的仿真，并结合仿真图进一步讨论了每种方法的估计质量。
从本篇论文可以看出，BT法先利用观测数据求出信号自相关函数的估计量，然后对其进行傅里叶变换，得出功率谱估计。它是功率谱密度的一致估计量，但是效率较低。周期图法直接对观测数据进行傅里叶变换，从而求得功率谱估计，虽然效率较高，但它不是功率谱密度的一致估计，且估计性能较差，所以需要进行平均修正。此外，为了提高谱分辨率，还进行了加窗修正。AR模型法有效地避免了经典谱估计的缺点，且在分辨率等性能上能够获得较好效果。所以在实际应用中，AR 模型法被广泛采用。

1．本课题所涉及的问题及应用现状综述
功率谱估计(PSD) 是用有限长的数据来估计信号的功率谱, 它对于认识一个随机信号或其他应用方面来讲都是重要的, 是数字信号处理的重要研究内容之一，在军事，生物医学，通信等领域得到了较为广泛的应用。
功率谱估计可以分为经典谱估计(非参数估计) 和现代谱估计(参数估计)。前者的主要方法有BT PSD估计法和周期图法; 后者的主要方法有最大熵谱分析法(AR 模型法)、Pisarenko 谐波分解法、Prony 提取极点法、Prony 谱线分解法以及Capon 最大似然法。其中周期图法和AR 模型法是用得较多且最具代表性的方法。
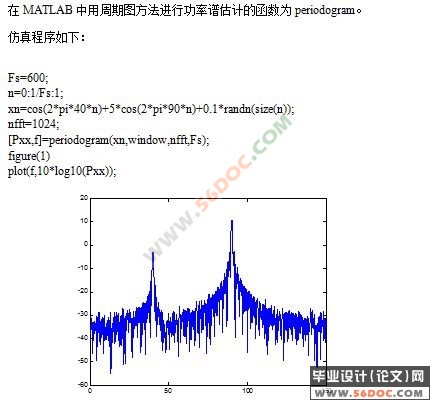
对于本课题来讲，应首先了解随机信号的基本知识，掌握信号与系统中傅里叶变换的相关知识，掌握MATLAB中一些基本语法，全面了解MATLAB中提供用于功率谱估计的函数。

2．本课题需要重点研究的关键问题、解决的思路及实现预期目标的可行性分析
本课题需要研究的关键问题是：
（1），研究掌握随机信号的基本理论；
（2），研究每种功率谱估计的方法。
（3），学习MATLAB的相关知识。
解决的思路：
（1）查看信号处理方面的书籍，复习关于随机信号的基本理论
（2）上网查找关于一些功率谱估计的资料并参考其中的一些方法，重点研究有关理论并进行分析。
（3）学习MATLAB的基本知识及用MATLAB进行功率谱估计的方法，了解每种方法的优缺点，并针对被估计信号的特点选择合适的方法。

预期目标的可行性分析：
        本课题要求对随机信号、信号与系统、MATLAB等学科的知识有较全面的了解，在大学期间，对随机信号分析，MATLAB这两门课程已有初步了解，对信号与系统了解较深，在导师的指导下，完成本课题是完全有可能的。

3．完成本课题的工作方案
完成本课题要认真学习信号处理、随机过程的相关知识，掌握随机信号功率谱估计基本原理和计算机仿真的基本方法，并对其进行谱估计有一个清晰的认识，故应复习随机信号基本理论和MATLAB语言的使用。为此制定完成本课题的工作方案如下：

第 3 周        熟悉随机信号的基本理论知识
第 4 周         复习信号与系统中的相关知识，提交开题报告
第5～6周         学习谱估计的基本方法。
第7～8周         阅读相关参考文献。
第9～10周     学习MATLAB的相关知识。
第11～12周    对谱估计的每种方法进行仿真。
第 13 周         总结仿真结果，写出论文初稿。
第 14 周       对毕业论文进行修改，并进行后期检查。
第 15 周       总结、完成毕业设计论文。
第 16 周       完成毕业设计答辩。

目录  11000字
摘要    I
ABSTRACT    II
1  引言    1
2 随机过程及估计理论基本知识    2
2.1 随机过程的基本知识    2
2.1.1  随机过程的分类    2
2.1.2  离散随机过程的数字特征    2
2.2  离散随机过程的功率谱密度    3
2.2.1  离散随机过程功率谱密度定义    3
2.2.2  随机过程功率谱密度的性质    4
2.2.3  功率谱密度与自相关函数的关系    4
2.3  估计量的评价标准    4
2.3.1  无偏性    4
2.3.2  有效性    5
2.3.3  相合性    5
3  经典谱估计及其仿真    5
3.1  周期图    5
3.1.1  周期图的定义    5
3.1.2  周期图的性能    7
3.1.3  平均周期图    9
3.1.4  加窗周期图    10
3.1.5  周期图的仿真    12
3.1.6  平均周期图的仿真    13
3.1.7  加窗周期图的仿真    14
3.2  BT法    16
3.2.1  BT法    16
3.2.2  BT法的仿真    19
4  AR模型法    21
4.1  AR模型法的基本理论    21
4.1.1  AR模型的Yule-Walker方法    22
4.1.2  AR模型的协方差方法与修正协方差方法    22
4.1.3  burg递推法    25
4.2  AR模型法的仿真    25
4.2.1  Yule-Walker方法    25
4.2.2  协方差方法与修正协方差方法    26
4.2.3  burg递推法    27
4.2.4  AR模型阶的选择    28
5  结论    30