矩阵分解及其应用

矩阵分解及其应用(论文8000字)
摘  要：数学这一基本学科在自然科学发展中是最早，最基础、最为精华的学科之一，而矩阵是数学中不可或缺的一环。在一些数据繁冗的矩阵运算中就是以普通的矩阵相乘的方式来表示一个数据总量宏大的矩阵，相应的就减少了计算难度，这就是矩阵分解的主要目的。
本文主要介绍了矩阵分解的三种常用分解方式：三角分解法、QR分解法和奇异值分解法。文中详细给出了每种分解的理论依据以及常用方法，并利用实际例子进行的验证。在文章的最后，我们运用C++编译程序编程实现了矩阵的LU分解，同时给出了程序框图及程序源代码，并利用实际矩阵进行了验证。
关键词：矩阵分解；三角分解法；QR分解法；奇异值分解法；应用；

The Decomposition of Matrix and It's Adhibition
Abstract: Mathematics is one of the most extraordinary and fundamental subjects which is founded earliest in science.Matrix is an important branch of math.The decomposition of matrix is converting a complex matrix into the product of some simple matrices.And this is the purpose of matrix decomposition.
The contents of this paper include three commonly used decomposition methods of matrix decomposition about triangular factorization,QR factorization and singular value decomposition.In the end this thesis developed the computer programs by C++ compiler to achieve the whole computing processes of LU decomposition.Then we give the process diagram and pass the program test.
Keywords: matrix decomposition;triangular factorization;QR factorization;singular value decomposition;
application
 

目  录    2
摘  要    4
Abstract:    5
一、绪论    6
1.1 论文的研究意义    6
1.2 论文的研究思路    6
1.3 国内外研究的现状    6
1.4 论文的研究内容    7
二、矩阵的三角分解法    8
2.1 矩阵三角分解的概念及定理    8
2.2 矩阵三角分解的常用方法及应用举例    9
2.2.1  （高斯）消元法    9
2.2.2  （杜利特尔）分解法    12
2.2.3  （乔列斯基）分解法    13
三、矩阵的 分解法    14
3.1 矩阵 分解的基本概念及定理    14
3.2 矩阵 分解的常用方法及应用举例    15
3.2.1 利用 正交化方法    15
3.2.2  （吉文斯）变换法    16
3.2.3  变换求矩阵的 分解    18
3.2.4 利用初等变换求矩阵的 分解    19
3.2.5 利用行(列)初等变换法    21
四、矩阵的奇异值分解    22
4.1 矩阵奇异值（ ）分解的概念及定理    22
4.2 矩阵奇异值分解的常用方法及应用举例    23
五、矩阵分解的程序实现    24
5.1 矩阵分解编程的意义    24
5.2 矩阵分解的算法思想    24
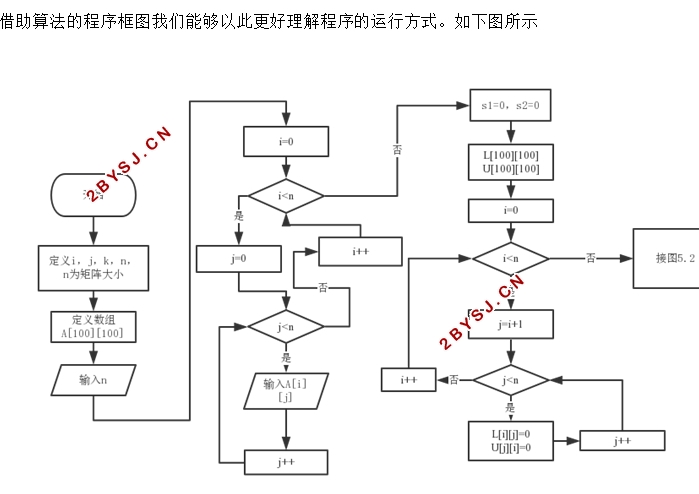
5.3 程序框图    25
5.4 程序代码    27
5.5 程序测试    29
六、结语    32
参考文献    33
致谢    34