基于蚁群算法的航班着陆排序(附仿真代码)☆

摘要
当空中交通拥挤时，对航班的着陆顺序进行适当调整，可以缓解拥挤，减少航班延误，提高飞行安全性。本文将蚁群算法用于着陆航班的排序问题。首先，建立以航班延误总时间最小为目标的规划模型，将航班着陆排序问题转化为非对称的TSP问题。然后，用蚁群算法寻找符合实际操作的优化排列；最后，选取某机场某段时间的航班时刻表进行实际数据的仿真计算。本文应用的算法具有较好的有效性和较强的实用性。
关键词：着陆航班；蚁群算法；排序
 
Abstract
Adjusting the schedule of landing flights can reduces air traffic congestion and flight’ s delay in air, and also can improves the safety of flying when air traffic congestion happens. In this paper, ant colony algorithm (ACO) was applied to solve the prioritizing problem of flight landing. First, an objective programm was developed basedon the minimum total delay cost, and converted the problem to an asymmetric TSP program.Then, a practice flight prioritizing can be derived with ACO. At last, select a certain period of time of an airport flight schedules of actual data for the simulation. The algorithm of this article has a better practical effectiveness.
Key words: scheduling landing flight;ACO;prioritizing

问题描述
在空管工作中，许多机场都会遇到在同一时间范围内，有多架飞机进出的情况。在空中交通高峰时期，空中交通管制员必须确保每一架飞机应保持的安全程度，决定飞机所使用的航路以及正确的机动方式。当对航路和空域占用的需求可能达到或超过系统容量时，经常需要采用延迟策略。由于机型、天气及人的因素等综合影响，多架航空器到达机场的过程是一个动态的过程。其进近次序及每架航空器所需的最短延误时间并不能从雷达信息中直接得到。
我们讨论的排序问题，主要是针对两个成功登陆飞机间的最小允许间隔和着陆速度以及序列的排序。事实上，在考虑先到先服务（FCFS）原则的基础上，从不同类型飞机必须保持不同的“最小安全间隔”（为了简化模型，最小安全间隔只考虑尾流间隔）入手，通过对飞机队列次序的重新排列，对所有可能的飞机排序方式进行搜寻，找到一种成本（指队列中每两架飞机之间所需时间间隔的总和或以等待时间为参数的每架飞机的等待成本的总和）最小的排队次序，即是该组飞机的最佳排序方案。
由于受各方面因素的影响，以经验公式和个人判断得到的进近次序缺乏精确的理论计算，有时甚至会影响交通流量，形成人为的交通拥挤和航班延误，造成不必要的空中等待，大大降低了空域的使用率。理论上探讨进近航班的进近次序，给管制员的主观判断提供理论依据，有利于提高终端管制的运行效率。
当航班为n架次时，其下降的顺序全排列的情况有n!种。因此，当航班架次较多时计算量很大，甚至造成计算机因计算溢出而瘫痪。另外，由于管制设备与水平等原因，在实际情况中对航班的位置进行大调整也是不现实的。所以，全排列中的许多种排列情况可以不予考虑。
对进近着陆航班进行排序，国内外有大量的研究，其中比较典型的有滑动窗排序、单机排序、动态排序等。当着陆航班的数目比较大的时候，这些方法的寻优进程比较缓慢，而且易陷入局部最优解。蚁群算法是对自然界蚂蚁的寻径方式模拟而得出的一种仿生算法。它具有分布式、正反馈机制和贪婪式搜索的优点，具有很强的搜索能力，不易陷入局部最优解，而且能很快地得到全局最优解。[11]
因此，如何用蚁群算法建立航班地面等待模型，如何利用实际的数据进行仿真测试与分析，是拟解决的关键性问题。不考虑天气，机型，人为等诸多因素影响，对航班的降落次序位置按照经蚁群算法求解后的最优次序进行重新排列，使得由于交通拥挤造成航班延误所带来的影响最小。

数学规划模型
排序问题在数学上可表述为某一目标函数的最小化问题，目标函数与每架飞机的延迟时间相关，并受最小飞行间隔的约束。
设在空中拥挤时，n架航班的到达机场的初始顺序是g，它们在时间段[0, T]内进近。在安全间隔容许的情况下，以总的航班延误时间最少为原则对着陆航班进行重新排序，顺序为{As1，As2，…，Asn}。
令tei 表示航班Ai 预计着陆时刻；tsi 表示航班Ai实际着陆时刻；ci 表示航班Ai 的单位延迟费用（包括由于延迟对本身航班的损失和对后续航班的影响）；si 表示航班排序后的位置。
以总的航班延误最少为目标建立规划模型为：
 
 si – i < g
 i=1,2,…,N   j=1,2,…,N
si – i < g表示航班i 排序前后的位置差，在计算目标函数时，如果si – i< g，则令ai=0，表示提前降落的航班的延迟费用和对后续航班的影响为0。si – i < g航班排序的位置约束，即航班i只能提前或则推后几个位置。这个约束条件主要考虑到飞机性能、管制员的负荷以及先到尽量先服务的公平原则等等，根据不同的要求选择不同的g值。本文在尽量满足FCFS算法原则的前提下选择g为3。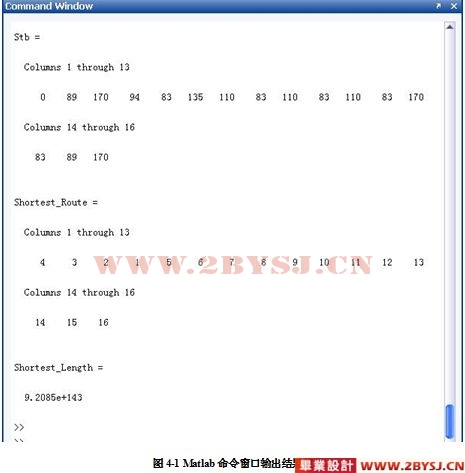





目  录
摘要 I
Abstract II
1 引言 1
1.1问题的提出 1
1.2 航班着陆排序算法的研究现状 1
1.3 本文框架 2
2 蚁群算法 4
2.1蚁群算法基本原理 4
2.2基本蚁群系统模型 5
2.3基本蚁群算法的实现步骤 6
2.4蚁群算法的应用 7
(优秀毕业设计:www.2bysj.cn)
3 基于蚁群算法航班着陆的排序方法 8
3.1问题描述 8
3.2 数学规划模型 8
3.3 方法步骤 9
3.4 程序流程图 11
4 算法仿真 13
4.1数据与参数选择 13
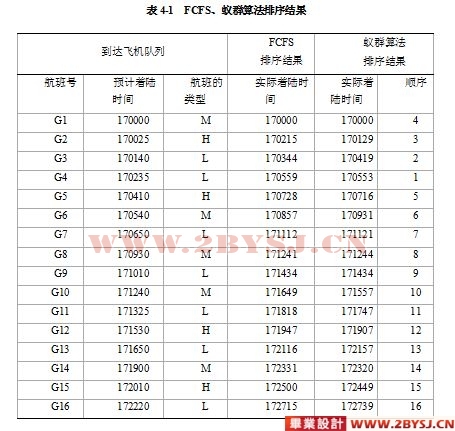
4.2 程序运行结果 13
4.3 结果分析 15
5 结论 17
参考文献 18
致谢 19
附录A 基于蚁群的着陆航班排序仿真代码 20

附录A  部分仿真代码
%Matlab程序代码
%初始化
m=16;      %%蚂蚁个数
Alpha=1;  %信息素重要程度的参数
Beta=10;%启发式因子重要程度的参数
Rho=0.01;%信息素蒸发系数
NC_max=50;%%最大迭代次数
Q=1000; %蚂蚁完成一次完整路径搜索所释放的信息素的总量
C=[0 0;0 25;0 100;0 155;0 250;0 340;
    0 410;0 570;0 610;0 760;0 805;0 930;
    0 1010;0 1140;0 1210;0 1340]; %C(:,2)为ETA预计到达时间
dis=[94 83 83;110 89 89;170 135 113]; %尾流间隔
ci=[1,1.5,2,3,1,1,2,1,1.5,2,1.5,1.5,2,1,2,1.5]; %表示航班i的单位延迟费用
type=[2 3 1 1 3 2 1 2 1 2 1 3 1 2 3 1]; %飞机类型
%变量初始化
n=size(C,1);%n表示问题的规模
D=zeros(n,n);%D表示完全图的赋权邻接矩阵
for i=1:n  
    for j=1:n
        if (i~=j)
        D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5; %计算距离
        else
        D(i,j)=eps;
        end
    D(j,i)=D(i,j);
    end
end
...